Задачи планирования последовательности действий
Многие результаты в области ИИ достигнуты при решении " задач для робота ". Одной из таких простых в постановке и интуитивно понятных задач является задача планирования последовательности действий, или задача построения планов.
В наших рассуждениях будут использованы примеры традиционной робототехники (современная робототехника во многом основывается на реактивном управлении, а не на планировании). Пункты плана определяют атомарные действия для робота. Однако при описании плана нет необходимости опускаться до микроуровня и говорить о датчиках, шаговых двигателях и т. п. Рассмотрим ряд предикатов, необходимых для работы планировщика из мира блоков. Имеется некоторый робот, являющийся подвижной рукой, способной брать и перемещать кубики. Рука робота может выполнять следующие задания (U, V, W, X, Y, Z - переменные).
goto(X,Y,Z)перейти в местоположение X,Y,Z
pickup(W)взять блок W и держать его
putdown(W)опустить блок W в некоторой точке
stack(U,V)поместить блок U на верхнюю грань блока V
unstack(U,V)убрать блок U с верхней грани блока V
Состояния мира описываются следующим множеством предикатов и отношений между ними.
on(X,Y)блок X находится на верхней грани блока Y
clear(X)верхняя грань блока Х пуста
gripping(X)захват робота удерживает блок Х
gripping()захват робота пуст
ontable(W)блок W находится на столе
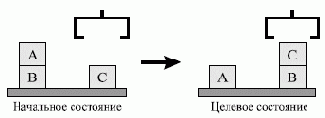
Рис. 3.8. Начальное и целевое состояния задачи из мира кубиков
Предметная область из мира кубиков представлена на рис. 3.8 в виде начального и целевого состояния для решения задачи планирования. Требуется построить последовательность действий робота, ведущую (при ее реализации) к достижению целевого состояния.
Состояния мира кубиков представим в виде предикатов. Начальное состояние можно описать следующим образом:
start = [handempty, ontable(b), ontable(c), on(a,b), clear(c), clear(a)]
где: handempty означает, что рука робота Робби пуста.
Целевое состояние записывается так:
goal = [handempty, ontable(a), ontable(b), on(c,b), clear(a), clear(c)]
Теперь запишем правила, воздействующие на состояния и приводящие к новым состояниям.
(




(



ontable(X)

(



((on(X,Y)



(



((clear(Y)



Прежде чем использовать эти правила, необходимо упомянуть о проблеме границ. При выполнении некоторого действия могут изменяться другие предикаты и для этого могут использоваться аксиомы границ - правила, определяющие инвариантные предикаты. Одно из решений этой проблемы предложено в системе STRIPS.
В начале 1970-х годов в Стэнфордском исследовательском институте (Stanford Research Institute Planning System) была создана система STRIPS для управления роботом. В STRIPS четыре оператора pickup, putdown, stack,unstack описываются тройками элементов. Первый элемент тройки - множество предусловий (П), которым удовлетворяет мир до применения оператора. Второй элемент тройки - список дополнений (Д), которые являются результатом применения оператора. Третий элемент тройки - список вычеркиваний (В), состоящий из выражений, которые удаляются из описания состояния после применения оператора.
Ведя рассуждения для рассматриваемого примера от начального состояния, мы приходим к поиску в пространстве состояний. Требуемая последовательность действий (план достижения цели) будет следующей:
unstack(A,B), putdown(A), pickup(C), stack(C,B)
Для больших графов (сотни состояний) поиск следует проводить с использованием оценочных функций. Более подробно о работах по планированию, в том числе современные публикации по адаптивному планированию, можно прочитать в литературе [7], [47], [48], [49], [50].
В качестве заключения по данному разделу лекции следует сказать, что планирование достижения цели можно рассматривать как поиск в пространстве состояний. Для нахождения пути из начального состояния к целевому (плана последовательности действий робота) могут применяться методы поиска в пространстве состояний с использованием исчисления предикатов.
