Компенсация статической нагрузки на привод
Компенсация статической нагрузки на привод , расположенный в сочленении E, реализуется выбором соответствующего управления исполнительным приводом в сочленении D.Для компенсации только статических нагрузок рассматривается установившийся режим работы системы, когда левые части уравнений (14.1) и (14.2) равны 0
0=MqП-M






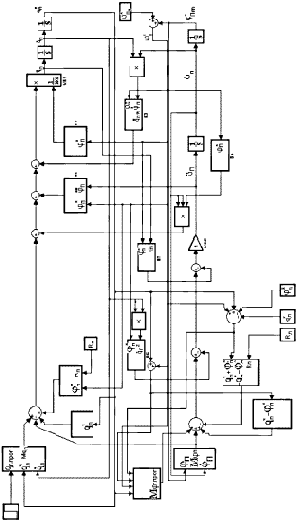
Рис. 14.3.
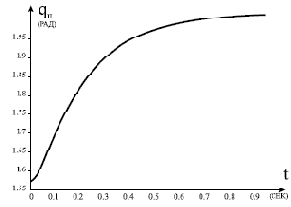
Рис. 14.4.
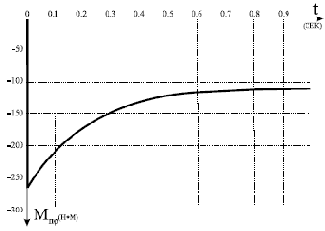
Рис. 14.5.
Из (14.3) вычисляется M


M


Для построения системы управления пятизвенником (рис. 14.1) составим систему уравнений,описывающую динамику левой кинематической цепи
B8q''Л+B9









где
B8=J1+2A6+2A7cos





m2 - масса звена 2; L1 и L2 - длина звеньев 1 и 2; Jц2 - момент инерции звена 2 относительно центра масс Ц2.
Компенсировать статические нагрузки на привод, расположенный в сочленении A, также возможно выбором соответствующего управления исполнительным приводом, установленным в сочленении B. Для компенсации только статических нагрузок рассматривается установившийся режим работы системы, когда левые части уравнений (14.6) и (14.7) равны 0
0=MqЛ-M






Из (14.8) вычисляется M


M



В уравнениях (14.5) и (14.10) неизвестны RП и RЛ. Реакция связи RП и RЛ определятся из решения системы уравнений, составленной из (14.4) и (14.9), в которых M




a1RП+b1RЛ=C1, a2RП+b2RЛ=C2, (14.11)
где
a1=L4sin










Из решения (14.11) получим
RП=(C1b2-C2b1)/(a1b2-a2b1), RЛ=(C2a1-C1a2)/(a1b2-a2b1).
